A PartiMap a K-Monitor innovatív, ingyenes, nyílt forráskódú térképes kérdőív-alkalmazása, amely egyszerű használatával és átlátható működésével könnyíti a helyi fejlesztések társadalmasítását. 

Az eszköz nemcsak az adatgyűjtést gyorsítja fel, hanem a begyűjtött információk elemzésében is támogatást nyújt. Hogyan lehet egy kérdőíves felmérésből értékes adatokat kinyerni? Milyen módszerekkel érhetjük el, hogy az eredmények valóban tükrözzék a közösség igényeit? Bemutatjuk az adatkezelés alapjaitól egészen az elemzési stratégiákig a kérdőív lezárása utáni foylamatot. 

Ez a blogposzt egy gyorstalpaló azoknak, akik szeretnének a PartiMap-pal kérdőívet készíteni, de még nem rutinosak a kérdőívre beérkezett adatok elemzésében. 

Ha ahhoz keresel segítséget, hogy hogyan rakj össze egy kérdőívet a PartiMap segítségével, arról itt találsz bővebb információt. 

Adatkezelési szempontok

Amikor egy projekt során személyes adatokkal dolgozunk – legyen szó adatgyűjtésről, feldolgozásról vagy megosztásról –, különösen fontos az adatvédelmi és etikai szempontok figyelembevétele. Még ha az információk nyilvánosan hozzáférhetők is, az érintettek magánszférájának tiszteletben tartása elengedhetetlen. A felelős adatkezelés alapelvei – mint az átláthatóság, az adatminimalizálás, a célhoz kötött adatfelhasználás, valamint az érintettek hozzájárulásának tiszteletben tartása – segítenek biztosítani, hogy az adatgyűjtés ne járjon az egyének jogainak és biztonságának sérülésével. A The Engine Room ajánlásai alapján az adatokkal való munka során nemcsak a jogi megfelelésre, hanem az etikus döntéshozatalra is törekedni kell – különösen akkor, ha az adatok érzékeny társadalmi, politikai vagy közösségi kérdésekhez kapcsolódnak.

Adatbázis megismerése

PartiMap szoftverünket úgy terveztük, hogy használata egyszerű, minden korosztály számára érthető és átlátható, továbbá logikus legyen. A papírra vetett kérdőívektől viszonylag rövid út vezet az adatfelvételig, tehát addig a pontig, amíg elkezdjük terjeszteni a kérdőíveinket. De mi történik az adatfelvétel lezárása után? Hogyan elemezzük az adatokat?

Amennyiben kérdőíves felmérés eredményeiből származó adatbázishoz jutunk, érdemes először felmérni az adatbázisunk felépítését. Általában egy sor egy válaszadót jelent és minden oszlop egy-egy változót (A változó a közvélemény-kutatásban egy olyan mérhető jellemző vagy tulajdonság, amely a válaszadók közötti különbségeket írja le, és amelynek értékei a kutatás során rögzíthetők és elemezhetők. A változók lehetnek például életkor, nem, politikai vélemény, szavazási hajlandóság vagy elégedettség egy intézménnyel kapcsolatban.). Ezek a változók egyrészt a kérdőív kérdései, másrészt pedig lehetnek olyan segédváltozók, mint például, hogy mikor vagy milyen eszközről töltötte ki a válaszadó a kérdőívet.

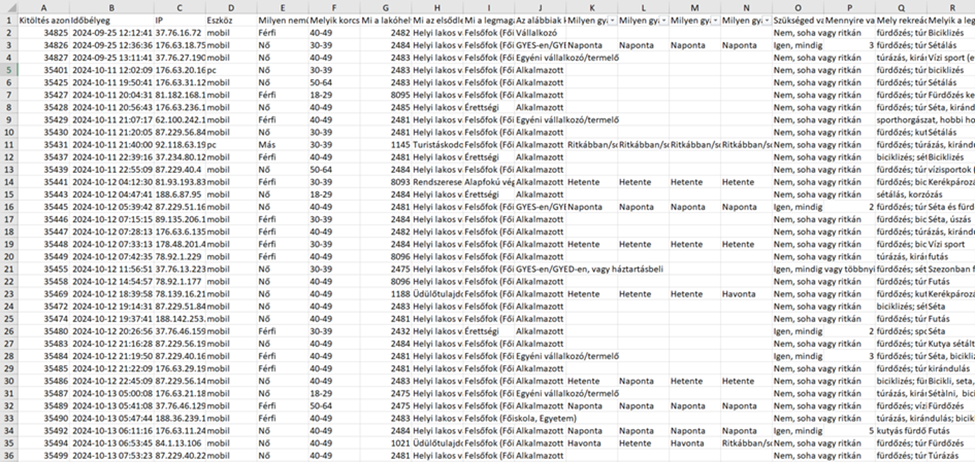
Beérkező eredmények a PartiMap riportjában

Állapítsuk meg először az elemszámot, vagyis, hogy mennyi válaszadót tartalmaz az adatbázisunk. A különböző kérdésekre adott válaszoknál előfordulhat, hogy bizonyos kérdéseket nem kapott meg minden válaszadó (például csak a munkavállalóktól kérdezték meg, hogy milyen szektorban dolgoztak), vagy akár az is, hogy válasz nélkül továbblépett a kérdésen a válaszadó. Ezek megállapításához ismerni kell a kérdőív programozását (azt a felületet, ahova a kérdéseket írjuk és sorbarendezzük), ugyanakkor adatelemzésnél a kérdésekre adott válaszok számából is levonhatunk következtetéseket. A kitöltők számának megállapításához keressünk egy olyan változót, amelyben biztosan minden válaszadónak van értéke (például kitöltés ideje vagy válaszadó azonosítója), és jelöljük ki a teljes oszlopot. Az Excel-program a jobb alsó sarokban feltünteti a cellák számát, amennyiben az adatbázis tartalmaz fejlécet, akkor a cellák számából egyet kivonva megkapjuk a kitöltők számát.

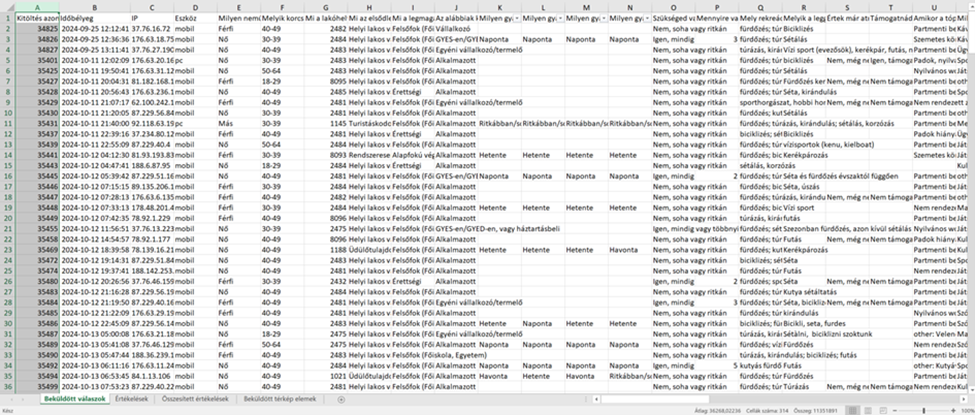
A oszlop, a kitöltések azonosítója

Alapvető demográfiai változók

Mielőtt nekifognánk a kérdőív érdemi kérdéseinek elemzéséhez, mérjük fel, hogy milyen a mintánk összetétele, vagyis, hogy a válaszadóink milyen demográfiai tulajdonságokkal rendelkeznek. Amennyiben egy reprezentatív mintával van dolgunk, akkor a különböző demográfiai megoszlásoknak a teljes sokaságban mért valós megoszlásokat kell tükrözniük. Amennyiben eltérés van, azt súlyozással szokás korrigálni. A reprezentativitás azt jelenti, hogy a mintánkban vett megoszlások megegyeznek (vagy megközelítik) az alapsokaságban (azoknak az embereknek az összessége, akikről a kutatás során információt szeretnénk kapni) vett megoszlásokat különböző ismérvek mentén (általában nem, életkor, iskolai végzettség, településtípus és régió, ha országos felmérésről van szó). Amennyiben többek között ennek is megfelel a mintánk (ezen túl fontos még a véletlenszerűen vett minta, vagyis hogy az alapsokaság minden tagja egyenlő eséllyel kerülhessen a mintába), akkor a mintában mért eredményeket kivetíthetjük az alapsokaságra is, tehát a kutatás eredményei érvényesek lehetnek például egy település teljes lakosságára is. Tehát ha a magyar felnőtt lakosság 52%-a nő, akkor egy 1000 fős reprezentatív mintában körülbelül 520 nőnek kell szerepelnie. Ha nem reprezentatív mintával van dolgunk, vagy nem ismerjük a teljes sokaság ismérveit, akkor is érdemes áttekinteni, hogy milyen jellemzői vannak a válaszadóknak. Az alapvető demográfiai ismérvek közé tartozik a nem, az életkor, a lakóhely és az iskolai végzettség. Ezek az ismérvek kutatástól függően még kiegészülhetnek egyéb demográfiai jellemzőkkel (például családi állapot vagy munkaerőpiaci státusz).

Gyakoriság, megoszlás

Az Excel programban a legegyszerűbben Pivot-tábla használatával állapíthatunk meg egyszerű megoszlásokat (például azt, hogy a minta hány százaléka férfi és hány százaléka nő). Ehhez jelöljük ki az oszlopot, ami az elemezni kívánt változót tartalmazza és kattintsunk a „Beszúrás” fülön a „Kimutatás” ikonra, majd a felugró ablakban az OK gombra.

 Az automatikus beállításokat követve így egy új fület hozunk létre, amin megjelenik egy kimutatás tábla. A jobb oldalon megjelenő kimutatásmezők területen az általunk kijelölt változót láthatjuk. Ezt húzzuk be a tengely és az értékek területekre is, aminek eredményeképp megjelennek a táblázatban az adatok, vagyis jelenlegi példánkban a férfiak és nők száma. Amennyiben a gyakoriság helyett a megoszlásukra vagyunk kíváncsiak, vagyis hogy a mintánk hány százaléka nő és hány százaléka férfi, akkor kattintsunk az értékek területen az Értékmező-beállítások menüpontra, azon belül az értékek megjelenítése fülre, ahol a legördülő menüben átállíthatjuk a normál értékmegjelenést „Végösszeg százaléka” megjelenítésre.

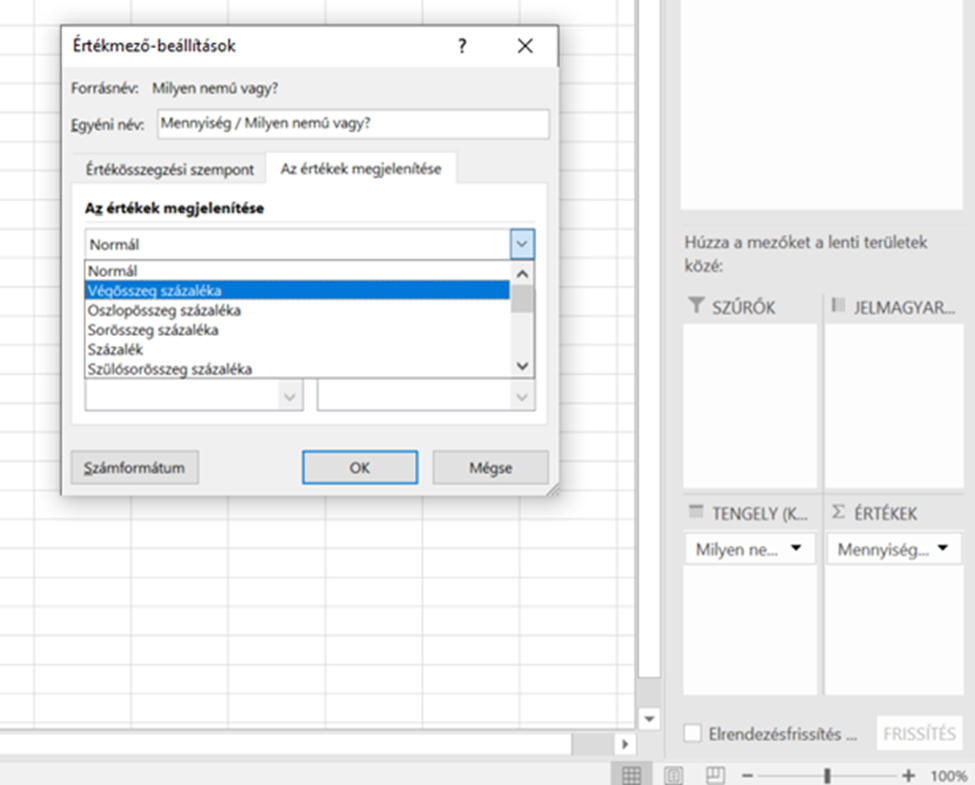
Az így létrejött táblázatból azt olvashatjuk ki, hogy a teljes mintánk hány százaléka férfi és hány százaléka nő. Ha az elemszámot és a százalékos megoszlást is szeretnénk látni egymás mellett, akkor nincs más dolgunk, mint kétszer odahúzni a változót az értékek területre és csak az egyik megjelenítését átállítani százalékosra. Az így létrejött táblázat az alábbi módon fog kinézni:

Ebből a táblázatból azt olvashatjuk le, hogy a mintánk 594 válaszadójából 221 férfi, 367 nő, ami azt jelenti, hogy a válaszadóink 62 százaléka nő, 37 százaléka pedig férfi. Hat darab válaszadó az egyéb kategóriát választotta, ami a minta 1 százalékát teszi ki.

Az többi alapvető demográfiai változót is vizsgáljuk meg hasonló módon, hogy átfogó képet kapjunk a válaszadóinkról.

Mérési szintek

Az előző példánkban egy úgynevezett nominális változót vizsgáltunk, vagyis olyan változót, amiben a lehetséges felvett értékek kategóriákat jelentenek (férfi és nő), amelyek nem számosíthatóak. Találkozhatunk olyan változókkal is, amik viszont számokat tartalmaznak (például az életkor, vagy az irányítószám). A statisztikában ezt mérési szintnek nevezzük, amiből négyet különböztetünk meg: nominális, ordinális, intervallum és arányskála.

A nominális mérési szintű változók esetében kategóriákról beszélünk, amik nem rendezhetőek sorrendbe és nincsen mértékegységük, így matematikai műveleteket nem végezhetünk velük. Ebbe a kategóriába esik a nem, vagy a megye/régió, ahol a válaszadó lakik. Az ilyen típusú változóknál egyszerű megoszlásokat számolhatunk.

• Például a kérdőívben ez a kérdés szerepel: „Mi az Ön neme?” A lehetséges válaszlehetőségek pedig azok, hogy „Férfi” vagy „Nő”. Tegyük fel, hogy 100-an válaszoltak a kérdőívben erre a kérdésre, ebből 53-an nők és 47-en férfiak. Ez azt jelenti, hogy a válaszadóink 53 százaléka nő, 47 százaléka férfi.

Az ordinális mérési szintű változó válaszlehetőségei sorrendbe rendezhetőek, viszont továbbra sincs mértékegységük és az értékek közötti különbség nem egyértelműen meghatározható, így ezekkel sem végezhetőek matematikai műveletek. Ordinális mérési szintű változó például az iskolai végzettség, vagy a település típusa (ami méret szerint sorrendbe rendezhető).

• Például a kérdőívben ez a kérdés szerepel: „Mi az Ön legmagasabb, befejezett iskolai végzettsége?” A válaszlehetőségek pedig azok, hogy „Legfeljebb 8 általános” vagy „Szakmunkásképző, szakiskola érettségi nélkül” vagy „Érettségi” vagy „Felsőfokú végzettség (főiskola, egyetem)”. Ezeket a lehetőségeket sorrendbe rendezhetőek, például tudjuk, hogy a diploma magasabb végzettség, mint az érettségi. Nincsen azonban mértékegységük, és nem meghatározható a kategóriák közötti különbség matematikailag, tehát például azt nem tudjuk, hogy hányszor magasabb végzettséget jelent a diploma megszerzése, mint az érettségié. Tegyük fel, hogy 100-an válaszoltak erre a kérdésre, amiből 18 főnek általános iskolai végzettsége van, vagy annál alacsonyabb, 23 főnek szakmunkásképzője érettségi nélkül, 35 főnek érettségije, 24 főnek pedig diplomája. Ez alapján azt mondhatjuk, hogy a kitöltők legnagyobb arányban érettségivel rendelkeznek, 35 százalékuk. 24 százaléknak diplomája, 23 százaléknak szakmunkásképzője van, 18 százaléknak pedig alapfokú iskolai végzettsége.

Az intervallum mérési szintű változók értékei számok, melyeknek van mértékegysége, összeadhatók és kivonhatóak és értelmezhető két érték közötti távolság, viszont nincsen egyértelmű kezdőpontja. Ilyen változó például a különböző skálákon mért kérdések (például egyetértés 1-5-ig tartó skálán). Az intervallum változók esetében a megoszláson kívül átlag is számítható.

• Például egy kérdőívben a következő kérdés szerepel: „Ön mennyire elégedett a szórakozási lehetőségekkel a településen, ahol lakik? Értékelje egy 1-5-ig tartó skálán, ahol az egyes azt jelenti, hogy egyáltalán nem elégedett, az ötös pedig azt, hogy teljes mértékben elégedett.” Képzeljük el, hogy 100-an válaszoltak erre a kérdésre, ebből 15-en egyest adtak, 10-en kettest, 40-en hármast, 20-an négyest és 15-en ötöst. Ebből számolhatunk megoszlást: 15 százalék egyáltalán nem elégedett, 10 százalék inkább nem elégedett, 40 százalék elégedett is, meg nem is, 20 százalék inkább elégedett, 15 százalék pedig teljes mértékben elégedett. Számolhatunk átlagot is ((15x1)+(10x2)+(40x3)+(20x4)+(15x5))/100=3,1, vagyis a válaszadók átlagosan 3,1-re értékelték a szórakozási lehetőségeket.

Az arányskála a legmagasabb mérési szint, ami abban különbözik az intervallum mérési szinttől, hogy van kezdőpontja, ami egyértelmű. Ilyen változó lehet például az életkor vagy az oktatásban eltöltött évek száma. A korábbiakhoz képest oszthatunk és szorozhatunk is az értékeivel.

• Például egy kérdőívben a következő kérdés szerepel: „Mi az Ön életkora?”. A válaszadó megadja az életkorát számokban. Ebből tudunk átlagot számolni, de mondhatjuk azt is, hogy például a kitöltők körében a nők átlagosan kétszer olyan idősek, mint a férfiak.

Számítások magas mérési szintű változók esetében

A szociológiai kérdőíves kutatásokban ritka az arányskála mérési szintű változók előfordulása, intervallum változókkal pedig leggyakrabban skálákon mért egyetértés, megítélés kapcsán találkozhatunk. Az arányskálára az életkor lehet példa ilyen kutatásokban, amennyiben nem korcsoportokra bontva kérdezték le a kérdőívben, hanem konkrét szám megadásával, akkor lehívhatjuk az átlagot, szórást, vagy percentiliseket a megfelelő képletekkel.

Az átlag értéke az adataink számtani középértékét mutatja meg, például mennyi az átlagéletkor a mintában. Az extrém értékek nagyban befolyásolják. Képlete: =ÁTLAG()

A szórás azt mutatja meg, hogy az adatok mennyire térnek el az átlagértéktől. Minél nagyobb a szórás, annál inkább eltérnek az adatok az átlagtól. Képlete: =SZÓRÁS()

A percentilis azt mutatja meg, hogy az adatok adott százaléka mekkora érték alá esik, például ha a 25. percentilis 40 az életkor esetében, az azt jelenti, hogy a válaszadók negyede fiatalabb 40 évesnél (háromnegyedük pedig idősebb). Képlete: =PERCENTILIS.KIZÁR()

Az elemzéshez azonban hasznosabb lesz, ha átalakítjuk az életkort ordinális változóvá, korcsoportokra bontva, például 18-29, 30-39, 40-49, 50-64, 65 felettiek. Ehhez szintén képleteket használhatunk, a példához az alábbit:

=HA(A2<=29; "18-29"; HA(A2<=39; "30-39"; HA(A2<=49; "40-49"; HA(A2<=64; "50-64"; "65+"))))

Ezzel átalakítottuk a kor változó mérési szintjét és így számolhatunk egyszerű százalékos megoszlást, valamint a kereszttáblákba is használható lesz az így létrehozott korcsoport változó.

Kereszttábla

Miután megismertük a mintánkat különböző demográfiai változók mentén, elkezdhetünk a kérdőív érdemi kérdéseivel foglalkozni. Itt is fontos megállapítanunk, hogy milyen mérési szintű változóval van dolgunk és ismét lehívhatunk egyszerű gyakoriságokat vagy megoszlásokat a korábban megismert módon. Az adatok további megismeréséhez használhatunk úgynevezett kereszttáblákat, ha két alacsony mérési szintű (nominális vagy ordinális) változó összefüggéseire vagyunk kíváncsiak. A kereszttáblák által megismerhetjük például, hogy a nők és a férfiak piacra járási szokásai között milyen eltérések vannak.

Ehhez jelöljük ki a nem változó és az elemezni kívánt változó (jelen esetben piacra járás gyakorisága) oszlopait a táblázatban, ismét kattintsunk a megszokott módon a Beszúrás fülre, azon belül a Kimutatások gombra és a felugró ablakban az OK gombra. Ezt követően az újonnan létrehozott fülön a kimutatásmezők részben húzzuk a nemet a sorok területre, a piacra járás gyakoriságát pedig egyszer az oszlopok területre, másodszor az értékek területre.

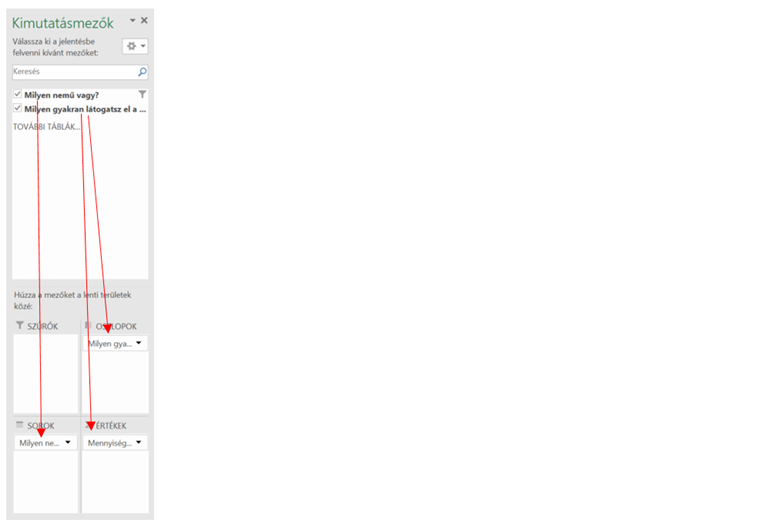
Az értékek területen kattintsunk a változóra, a felugró menüből válasszuk az értékmező-beállításokat, azon belül pedig az értékek megjelenítése fülön állítsuk át normál értékmegjelenítésről „Sorösszeg százaléka” lehetőségre. 

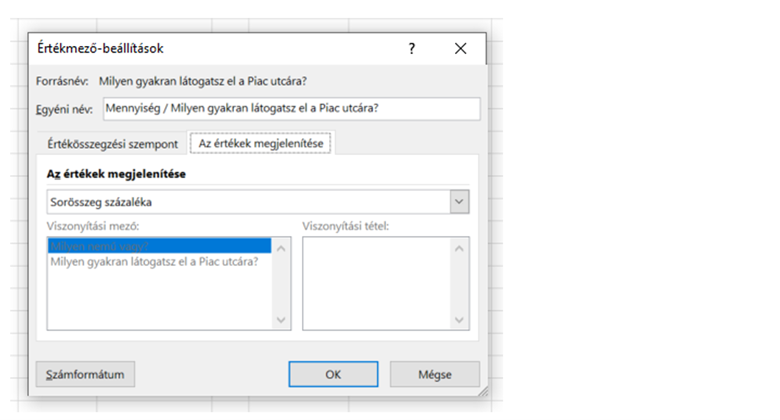
Az így létrejött táblázat az alábbi módon néz ki:

 
A táblázatban minden sor összege 100 százalék, vagyis azt olvashatjuk le például, hogy a nők hány százaléka látogatja napi szinten a Piac utcát. Ezen kívül a teljes minta megoszlása is látható a legalsó sorban.

A táblázatból azt olvashatjuk le, hogy az összes válaszadó 18 százaléka hetente egyszer, 33,5 százaléka hetente többször, 24 százaléka naponta, 25 százaléka pedig ritkábban látogatja a Piac utcát. A férfiak és nők hasonló gyakorisággal látogatják az utcát, a férfiak 26, a nők 24 százaléka látogatja ritkábban, mint hetente egyszer. A legalább hetente látogatók között van némi eltérés nemek szerint: a nők inkább csak hetente egyszer, vagy hetente többször látogatják az utcát (20 és 35 százalékuk), míg napi rendszerességgel 21 százalékuk. A férfiaknak viszont 27 százaléka látogatja naponta a Piac utcát.

Alacsony elemszám

Korábban már megvizsgáltuk a nem változó gyakoriságát és megoszlását, így tudjuk, hogy az egyéb kategóriába csupán 6 válaszadó esik. Ilyen alacsony esetszámnál nem érdemes a százalékos megoszlásokat figyelembe venni, mert félrevezető lehet (a táblázat celláinak számától függ, de körülbelül 30 elemnél kisebb kategóriákat nem érdemes egyénileg vizsgálni). Ilyenkor vagy nem foglalkozunk az adott kategória megoszlásaival, vagy összevonjuk egy másik kategóriával (ha képesek vagyunk az elemzéshez értelmes kategóriát létrehozni ilyen módon). Ehhez ismét képleteket kell segítségül hívnunk. Szúrjunk be egy új oszlopot a nem változó mellé, és az alábbi képlettel vonjuk össze a nőket és az egyéb kategóriába esőket:

=HA(VAGY(E2="Nő"; E2="Egyéb"); "Nő/egyéb"; "Férfi")

A táblázatból az is látszódik, hogy csupán egy válaszadó van a mintában, aki soha nem látogatja a Piac utcát, így ettől a kategóriától is megszabadulhatunk olyan módon, hogy összevonjuk a „ritkábban” kategóriával. Az elemzéshez bevonhatunk egyéb demográfiai változókat is, például az életkort, az iskolai végzettséget, és a szubjektív jövedelmi helyzetet. Az alábbi táblázat a Piac utca látogatásának gyakoriságának megoszlását mutatja nem, végzettség és szubjektív jövedelmi helyzet szerint.

Ezután értelmezhetjük az adatokat: egyrészt hasonlíthatjuk az egyes demográfiai kategóriákat a teljes minta átlagához. Például mondhatjuk azt, hogy az alapfokú végzettségűek nagyobb arányban járnak napi rendszerességgel a Piac utcába (33%), mint a teljes minta átlaga (24%). Másrészt hasonlíthatjuk egymáshoz a változók ismérveit, például összehasonlíthatjuk a nőket és férfiakat: a férfiak nagyobb arányban járnak inkább napi rendszerességgel a piac utcába, mint a nők, akik inkább heti szinten látogatják az utcát. Harmadrészt kereshetünk tendenciákat az ordinális (sorba rendezhető) változók esetében, például iskolai végzettségnél. Megállapíthatjuk, hogy minél alacsonyabb az iskolai végzettsége a válaszadónak, annál gyakrabban jár napi szinten a Piac utcába.

Skálán mért, ordinális változók

 Az olyan kérdéseknél, ahol a válaszadónak valamilyen skálán kell értéket választania, (például 1-5-ig mennyire elégedett egy adott szolgáltatással), számolhatunk átlagokat is. Ezt a teljes mintára is megtehetjük, illetve különböző demográfiai csoportok között is. Az átlagok segítenek abban, hogy gyorsan és egyszerűen össze tudjunk hasonlítani csoportok között értékeket, vagy különböző változók értékeit. Ha például öt különböző szolgáltatásról kértük ki a válaszadók véleményét, akkor az átlagok alapján könnyedén megmondhatjuk, hogy átlagosan melyik szolgáltatással a legelégedettebbek a válaszadóink.

Nézzünk egy példát erre! A Piac utcával kapcsolatban 15 szolgáltatásról kérdezték meg a válaszadókat, hogy mennyire elégedettek egy 1-5-ig terjedő skálán, ahol az egyes azt jelentette, hogy egyáltalán nem elégedett, az ötös pedig azt, hogy teljes mértékben elégedett. Alább láthatóak az átlagok:

A táblázatból azt olvashatjuk ki, hogy a közvilágítással a legelégedettebbek a válaszadók. Inkább elégedettek még a gyalogátkelők helyével, kialakításával, a járdák állapotával, a zaj mértékével, a közbiztonsággal, a köztisztasággal. Inkább nem elégedettek az épületek, padok állapotával, információkkal, kínálattal. A legkevésbé a levegőminőséggel, parkolók mennyiségével és növényzet mennyiségével elégedettek. Vizsgáljunk meg egy szolgáltatást demográfiai csoportok szerint!

Ehhez a megszokott módon kijelöljük a szolgáltatás megítélését és a demográfiai változókat (egyesével). A kimutatás fülön azonban a szolgáltatás megítélését csak az értékekhez húzzuk be, az oszlophoz nem. Az értékek területen, az értékmező beállítások alatt, az értékösszegezési szempont fülön átállítjuk, hogy az átlagok jelenjenek meg a táblázatban. Az alábbiakban a közbiztonság megítélésének átlagai olvashatóak, színezve érték szerint (táblázat kijelölése után a feltételes formázás fülön, a színskáláknál választható ki).

A táblázatból leolvashatjuk, hogy az összes demográfiai csoport közül az alacsony jövedelműek a legelégedetlenebbek a közbiztonsággal, a magas jövedelműek és a 40-49 évesek pedig a legelégedettebbek. Ne felejtsük el azonban, hogy az átlag nem ad teljes képet az egyes változókról, hiszen közepes átlagot eredményez az is, ha sok válaszadó jelöli a középértéket, és például az is, ha a válaszadók fele a legalacsonyabbat, fele pedig a legmagasabbat jelöli. Nézzük meg a közbiztonság korcsoportok szerinti megítélésének megoszlását!

Látható, hogy hiába a 40-49 évesek átlaga volt a legmagasabb, ha megnézzük a megoszlást, akkor az ő körükben a legmagasabb az elégedetlenek (1-es osztályzatot adók) aránya is. Milyen következtetést vonhatunk le ebből? A középkorúak megosztottak a közbiztonság kapcsán, többségük inkább elégedett, de egy jelentős kisebbség (12%) nem érzi magát biztonságban a Piac utcában.

Az ehhez hasonló, skálán mért kérdések esetében egyszerűsíthetünk az adatainkon az átlagszámításon kívül más módszerrel is, például összeadhatjuk az 1-es és 2-es lehetőségeket jelölőket egy inkább nem elégedett csoportba, illetve a 4-es és 5-ös értékeket jelölőket egy inkább elégedett csoportba. Így öt helyett, immár csak három kategóriát kell értelmeznünk. További egyszerűsítés lehet, ha kivonjuk az inkább elégedettek arányából az inkább nem elégedetteket, az alábbi táblázat ezt tartalmazza: 

Ebben a táblázatban a negatív értékek azt jelentik, hogy magasabb az elégedetlenek aránya, a pozitív értékek azt, hogy magasabb az elégedettek aránya egy adott demográfiai csoportban. Ez ismét az összehasonlítást könnyíti meg, hogy első pillantásra beazonosíthatóvá váljanak a szélsőséges véleménnyel rendelkező csoportok. Ha szeretnénk kommunikálni valamilyen eredményünket, akkor viszont érdemes visszatérni az eredeti ötfokú (vagy egyszerűsített háromfokú) skálához és például olyan megállapításokat tenni, mint hogy a válaszadók megosztottak a közbiztonság kapcsán: 37 százalékuk inkább elégedett, 30 százalékuk inkább elégedetlen.

Limitációk

Ha nem reprezentatív (és/vagy súlyozatlan) mintával dolgozunk, akkor nem vonhatunk le következtetéseket a sokaságra (például egy város lakóira), tehát nem mondhatjuk azt például, hogy a város lakóinak negyede elégedett a városvezetéssel, csupán azt, hogy a kérdőív kitöltőinek negyede elégedett.

Mire használhatjuk mégis az Excel programot adatelemzéskor? A kérdőívet kitöltők körében tehetünk megállapításokat, ami alapján hozhatunk stratégiai döntéseket is akár. Például azonosíthatjuk a leginkább fejlesztésre szoruló területeket, illetve azt is, hogy melyik demográfiai csoportok a legelégedetlenebbek bizonyos szolgáltatásokkal és ez alapján kikérhetjük az ő véleményüket célzottan. Például ha a legnagyobb problémát a padok hiánya okozza, és ezzel az idősebbek a legelégedetlenebbek, akkor célzottan fordulhatunk az idősekhez, hogy felmérjük az igényeiket.

Általános szempontok adatelemzésnél - összefoglalás

1. Gondolkodjunk milyen információk értékesek számunkra és ehhez igazítsuk az elemzést. Nem kell az összes változóval foglalkoznunk. Tegyük fel, hogy arra vagyunk kíváncsiak, hogy a férfiak és nők mit gondolnak egy közösségi térről. Azonosítsuk be, hogy melyik változókat fogjuk használni, például ebben az esetben a nem változót és az elégedettség változót.
2. Vizsgáljuk meg, hogy milyen válaszlehetőségei vannak a különböző változóinknak és döntsük el, hogy milyen műveletet végezhetünk el velük. A fenti példában például kiszámolhatjuk, hogy az összes kitöltő átlagosan 1-5-ig milyen osztályzatot adott, és aztán azt, hogy a férfiak és nők átlagpontszáma mennyi. De kiszámolhatjuk azt is, hogy a nők hány százaléka adott 5-ös osztályzatot és a férfiak hány százaléka adott 5-ös osztályzatot és ezt összehasonlíthatjuk.
3. Figyeljük meg, hogy a kérdőívben szereplő kérdések hogyan függenek össze egymással. Például megkérdeztük, hogy mivel tölti szabadidejét a válaszadó és a lehetőségek között szerepelt a sport is. Aztán egy másik kérdésben megkérdeztük, hogy milyen gyakran sportol. A két kérdés eredményeinek vizsgálatából levonhatjuk azt a következtetést például, hogy az idősebbek között magasabb arányban vannak olyanok, akik sportolnak, mint a fiatalok között, viszont a fiatalok gyakrabban sportolnak, mint az idősek.
4. Próbáljunk meg következtetéseket levonni az eredményeinkből. Tegyük fel, hogy a nők kisebb arányban elégedettek egy közösségi térrel, mint a férfiak és a kérdőívben arra is rákérdeztek, hogy különböző szempontok mentén hogyan értékelnék a közösségi teret a válaszadók. Összehasonlíthatjuk, hogy milyen szempontok esetében látunk eltérést a férfiak és nők véleménye között. Tegyük fel, hogy a nők a közösségi teret kevésbé tartják biztonságosnak, mint a férfiak. Levonhatjuk azt a következtetést, hogy a nők azért is lehetnek elégedetlenebbek az adott térrel, mert kevésbé érzik magukat biztonságban.
5. Ha meglepő eredményt kapunk, akkor ellenőrizzük, hogy biztosan semmi nem csúszott-e el a számításaink során, biztosan a megfelelő változókat vizsgáljuk-e, minden adat a helyén van-e, stimmelnek-e az elemszámok.

A cikk a Közösen Monitorozunk! projektünk keretében jött létre.

Másfél évvel ezelőtt 5 helyi civil szervezettel vágtunk neki a közös tanulásnak Közösen Monitorozunk! Projektünk keretében, ahol a cél a szervezetek érdekérvényesítési képességeinek fejlesztése és digitális kompetenciáik erősítése volt. A projektről részleteket itt találsz. 

Ha kérdésed lenne vagy vissza szeretnél jelezni nekünk a blogposztunkkal kapcsolatban, írd meg nekünk az info@k-monitor.hu címre!